自然界を支配する数理（フィボナッチ・ボロノイ）

昨日のWeb3・トレーディング講座でフィボナッチ比にふれました。チャート分析ではフィボナッチ比を多用します。フィボナッチ比で一番有名なのが皆さんもよくご存じの黄金比です。そしてフィボナッチ比の元になっているのがフィボナッチ数列です。

フィボナッチ比やフィボナッチ数列をご存知ないという方もまずは下の動画をご覧ください。とても美しい私のお気に入りの動画の一つです。内容的には前半がフィボナッチ、後半がボロノイ分割という内容になっています。

フィボナッチ

0　1　1　2　3　5　8　13　21　34　55　89　144　233　377　610　987・・・
と、直前の2つの数字を、0+1=1、1+1=2、1+2=3、2+3=5のように足して順番に並べたのがフィボナッチ数列です。これはイタリアの数学者レオナルド・フィボナッチがウサギの繁殖をヒントに考え出した数列だそうです。数学的に表現すれば以下のようになります。

F(0)=0
F(1)=1
F(n)=F(n−1)+F(n−2) (n≥2)

そして上の例でいえば、987÷610のように一つ手前の数字で割ったものがフィボナッチ比になります。このF(n)/F(n-1)のnを無限に続けると1.6180339887…と黄金比に収束していきます。また二つ手前の数字で割れば別のフィボナッチ比が導き出せます。例えばチャート分析では以下のようなフィボナッチ比がよく使われています。

F(n)/F(n-1)・・・1.618
F(n)/F(n+1)・・・0.618
F(n)/F(n-2)・・・2.618
F(n)/F(n+2)・・・0.382
F(n)/F(n+3)・・・0.236
F(n)/F(n-3)・・・4.236
F(n)/F(n-1)の平方根・・・1.272
F(n)/F(n+1)の平方根・・・0.786

フィボナッチ数やフィボナッチ比、それを元にしている黄金螺旋や黄金角（137.5度）は、人体から植物の生長、星雲にまで自然界のありとあらゆる場面に出現します。そのため、自然界や芸術、金融などさまざまな分野で応用されています。とても興味深いですよね！

ボロノイ分割

上記の動画の中でヒマワリの花が咲いた後からトンボの羽にかけてはボロノイ分割が描かれています。
ボロノイ分割は平面上の複数の点で、それぞれの2点間で垂直二等分線を引きます。その垂直二等分線でエリアを区切っていくと、下図のようなボロノイ図が描けます。

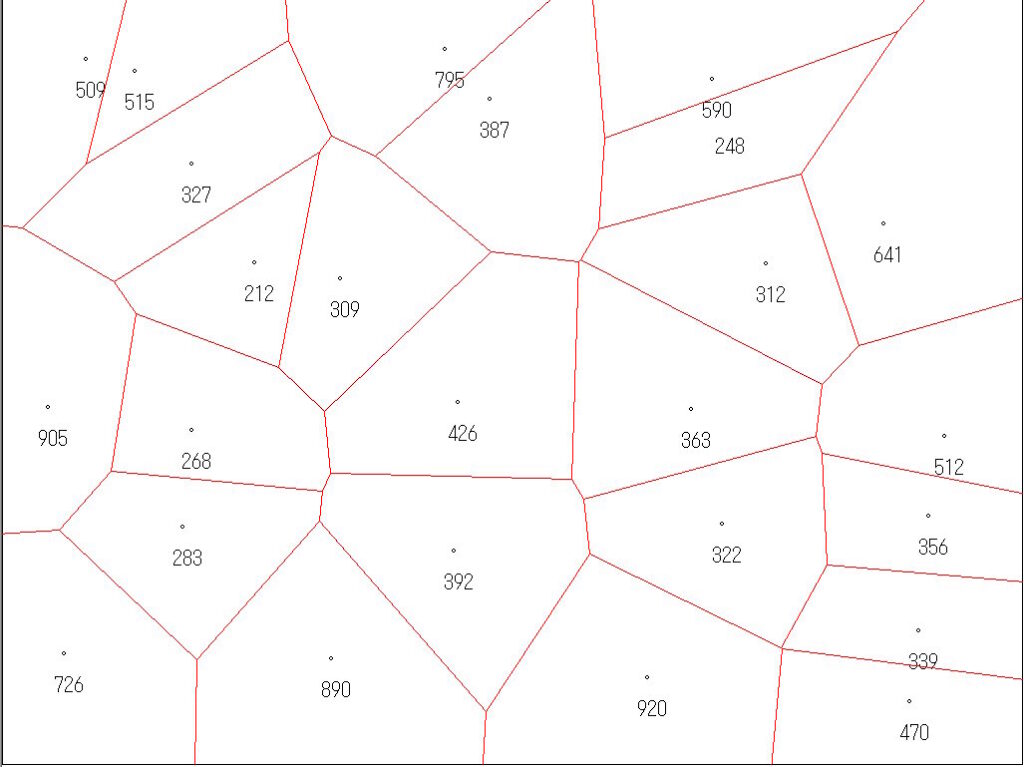
なんかちょっと細胞っぽいですよね。区切られたエリア内の任意の場所は他のどの点よりもエリア内の点に近いという特徴があります。ボロノイ図は上記動画のようにトンボの羽や皮膚の模様、動物の縄張り、植物の葉の配置パターンなど、様々なところに見られます。また、通信基地局の配置や施設の立地選定、サービス領域のモデリングなど、様々な利用がされています。

以下はとても興味深いボロノイ分割の実験動画です。不思議ですよね！是非ご覧下さい！

Web3・トレーディング講座では関連するところから、このように他分野のことも少し考えてみるきっかけのお話をさせていただくことがよくあります。また雑学講座でフィボナッチやボロノイ分割を扱う場合は、この内容をもう少し深く掘り下げて考えていきます。

shin MICの講座は特定の分野から様々な分野に広がっていくのが特徴です。

知的好奇心を原動力にshin MICで自分自身の知識と視野を広げてみませんか！？